機械学習モデルの解釈の入門: Partial Dependence Plot(部分依存グラフ)

背景

ビジネスかアカデミアかに関わらず、機械学習モデルを扱う際には、モデルの解釈が必要になることが多いです。今回は、機械学習モデルを解釈する手法の一つ、Partial Dependence Plotを紹介いたします。

※以下、Partial DependenceをPDと略します。

PDPlotのイメージ

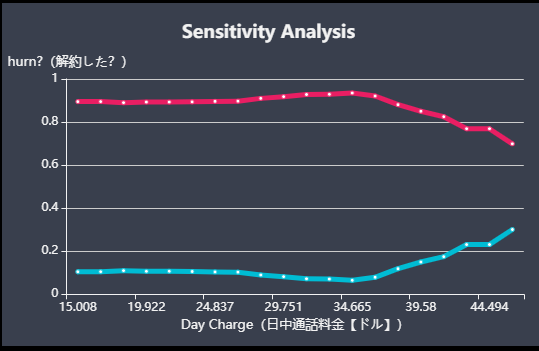
f:id:gri-blog:20201228153918p:plain

上の画像がPDPlotのイメージです（青線に着目してください。横軸：日中通話料金、縦軸：機械学習が予測した解約しやすさを表すスコア）。

これは、電話会社の顧客が次月契約を継続するかを予測するモデルにおける、日中通話料金という特徴量についてのPDPlotです。

PDPlotは、モデルにおける目的変数の対象特徴量への依存の仕方を表します。この例では、35ドル付近の時最も解約しにくく、50ドル付近が最も解約しやすい、ということを表しています。

これを定義から整理して正しく理解することが本記事の目的です。トップダウンに見ていくと見通しが良いので、本記事は以下の構成としました。

  • PDPlotの定義、仮定、計算方法
  • PDPlotの性質
  • PDPlotについてのまとめ

内容が繰り返しになってしまっている部分がありますが、数式を読むリテラシーにかなり幅があるので、丁寧に記述した結果そうなってしまっています。ご了承ください。

PD関数 \hat{f}_{x_S}の定義、仮定、計算方法

ここでは雰囲気だけ見ていただければ、定義の意味がよく分からなくても大丈夫です。

定義

\begin{equation}\hat{f}_{x_S}(x_S)= E_{x_C} [\hat{f}(x_S,x_C) ] = \int\hat{f}(x_S,x_C){\rm dP} (x_C) \end{equation}

式で使われている文字の意味

x_S : PDPlotを描く対象となる、1つか2つの特徴量、またはその値

x_C : モデルの他の特徴量、またはその値（ x_Sと x_Cの組み合わせで、特徴量全体となる）

E_{x_C}[ a ] : 特徴量 x_cの分布における変数  a の期待値

\hat{f} : 機械学習モデル 

仮定

x_Sと x_Cが独立

計算方法

\hat{f}_{x_S}(x_S)=\frac{1}{n}\sum_{i=1}^n\hat{f}(x_S,x^{(i)}_{C})

式で使われている文字の意味

n : 訓練データの件数

x^{(i)}_{C} : i 番目のデータの特徴量 x_Cの実際の値

PDPlotの性質

以下の記述のおおよそは、定義を観察しなければ理解できないので、定義に立ち返りつつ読んでいただければと思います。

定義の基本的なポイント

PDPlotを定義から一言で読み解けば、

  • 対象特徴量の予測スコアへの（Globalな）平均限界効果を表す
  • 平均限界効果の算出の仕方は、「他特徴量の分布を、対象特徴量の分布と独立に考えて確率平均を取ること」で見積もっている

ということだと思います。

「限界」は、日常的な意味で使われる「ギリギリの境」という意味ではありません。「限界」は「対象とする変数の変化だけ考慮したときの」という経済学的な意味です。例えば、限界利益（=固定費を度外視して変動費だけ考慮した利益）もこの経済的な意味で「限界」という言葉が使われています。

PDPlotの話に戻ると、もともと機械学習モデルは「全特徴量の値」→ 予測スコアという関数ですが、PDPlotは「対象特徴量の値」→ 平均予測スコアという関数になっていて、「対象特徴量の変化だけを考慮したときの」という意味で「限界」となっていることを確認できます。

その上で、Globalな（=全サンプルを考慮した上での）平均限界効果を算出する方法、つまり、モデルの引数から（全サンプルを考慮した上で）他特徴量の値を除く方法は、様々あり得ます。繰り返しになりますが、PDPlotでの方法は、他特徴量の分布を、対象特徴量の分布と独立に考えて確率平均を取るという方法です。（これは、 x_Sの値を人為的に固定し、その値がどんな値かに関わらず、実データの x_Cの分布のみに応じた確率平均を算出しているということです。）「独立に考えて」の部分を正当化するためには、対象特徴量がその他の特徴量と独立である必要があります（これゆえに、「 x_Sと x_Cが独立」という仮定をしています）。

この定義は、定義を見れば分かりますが、Globalな平均限界効果を考える上で最も単純な定義になっていると思います。

強みと弱み

上記「定義の基本的なポイント」を理解すれば自明ですが、強みと弱みについてまとめました。

強み
  • モデルにおけるGlobalな目的変数の対象特徴量への依存性を、特徴量と目的変数の因果関係として定量的に見積もっていること
  • 専門家でない人にとっても直観的に分かりやすいこと

このような強みは、「定義の基本的なポイント」を理解すれば分かることなので省略いたします。

弱み
  • x_Sと x_Cに相関があると、PDPlotの値はおかしくなること
  • x_Sと x_Cの交互作用が見られないこと
  • 対象の特徴量 x_Sの数は1つが見やすく、2つが限界なこと(2つだとやや見にくい)

2点目についてです。繰り返しになりますが、PDPlotは、対象特徴量 x_Sの目的変数への限界効果を表します。つまり、 x_Sと x_Cの組み合わせで目的変数へどう効くか（=交互作用）という情報はなくなっているということです。ただし、2つの特徴量の交互作用は、 x_Sとして2つの特徴量を選ぶことで見られます。

1点目も、2点目と同様に平均限界効果の算出の仕方が原因です。この原因の理解のための簡単な例として、 x_Sが身長で x_Cに体重が含まれ、身長と体重には相関があり、サンプルとしてAさん身長200cm体重90kg,Bさん150cm40kg,Cさん....がある場合を考えてみます。身長200cmについてのPDPlotの算出は、Aさん200cm90kg,B'さん「200cm」40kg,C'さん...という擬似的なサンプルを生み出して、それを機械学習モデルの入力として確率的平均を取ることでなされてしまいます。このように、機械学習モデルの学習データの身長体重の相関関係からしたらあり得ない（つまり、学習されていない）「200cm」40kgというサンプルが、PDPlotの値に寄与してしまっているのが問題です。

注意点
  • 機会学習モデルの予測精度が十分高くなければ、そもそもPDPlotが正しくならない
  • x_Sが疎なところで（一般に、機会学習モデルの予測精度が十分高くないので）PDPlotの値はおかしくなる
  • 現実世界での因果関係は必ずしも表さない

これらの原因は、PDPlotがモデルの出力をベースに算出していることです。そのため、これはPDPlot以外の解釈の手法でも同様に起きる問題です。

2点目はヒストグラムからこの問題が起きているか確認できます。

3点目について。よく使われるモデル（例えば決定木系のモデルや線形回帰などの統計モデルなど）では、そもそも特徴量と目的変数の因果関係を必ずしも表しません。そのため、そのPDPも特徴量と目的変数の因果関係を表しません。つまり、現実世界での因果関係は必ずしも表さない、ということです。

PDPlotのまとめ

PDPlotは、

  • 対象特徴量の予測スコアへの（Globalな）平均限界効果を表す
  • 平均限界効果の算出の仕方は、「他特徴量の分布を、対象特徴量の分布と独立に考えて確率平均を取ること」で見積もっている

 理解するためには、定義をよく観察する必要があります。

参照

Interpretability Methods in Machine Learning: A Brief Survey - Two Sigma

非常におすすめです。本記事は、上記内容を自分なりにまとめ直したものです。